“Her şey zıttı ile var olur.”
Zaman Makinesine hoş geldin! Bu ayki yolculuğumuz yine çok keyifli olacak. Hazırsan başlayalım!
Bu sefer zaman makinesi bizi çok uzaklara götürdü. Uzak Doğu’dayız ve olduğumuz yerden Çin Seddi’nin inşa edilmesini görebiliyoruz! Antik Çin’in, MÖ 1.700’lü yıllara kadar uzanan matematik serüvenini keşfedeceğiz.
Milattan önceki çoğu dönemde olduğu gibi bu dönemde de matematik günlük ihtiyaçları karşılamak ve hayatı kolaylaştırmak için kullanılıyordu. Ticaret, mühendislik, vergiler ve maaş hesapları konusunda matematikten faydalanılıyordu. Matematikte keşfettikleri şeyleri “Matematik Sanatı Üzerine Dokuz Bölüm” kitaplarında topladılar ve bu kitabı yeni nesillere matematik öğretmek için kullandılar. Daha önce Yin Yang felsefesini duymuş muydun? En azından sembolüyle karşılaşmışsındır. Bu kuram Çinliler tarafından ortaya atılmıştı. Çinliler, hayatta her şeyin zıttıyla var olduğuna inanır. Bu felsefelerini matematiğe de uyarlamışlar ve Avrupalılardan binlerce yıl önce negatif sayıların varlığını kabul etmişlerdi. Çin’de onluk sayı sistemi kullanılmaktaydı ve sayıları ifade etmek için bambu çubuklardan faydalanılıyordu. Pozitif ve negatif sayıların arasındaki farkı göstermek içinse farklı renkte çubuklar kullanıyorlardı. Ticarette kırmızı renk gelir, siyah renk ise gider anlamındaydı ve bu iki çubuk yan yana geldiğinde birbirini götürüyordu. Yani negatif ve pozitif sayılarla işlem de yapabiliyorlardı.
Daha sonra bambu çubuklarını kullanmayı bırakıp beşli gruplar halinde çizgiler kullanmaya başladılar. Böylece işlem yapmaları daha kolay oldu. Bu dönemde matematiğin ilerlemesini kısıtlayan şeylerden biri ise Çinlilerin sıfırın yerine kullanacak ifadelerinin olmamasıydı.
Çinliler; geometri, aritmetik, ikinci dereceden denklem çözümleri konusunda oldukça başarılıydı. Avrupa’da henüz kullanılmıyorken doğru, bileşik ve ters orantı işlemleri yapabiliyorlardı. Pisagor üçgeninin benzerlerini keşfetmişler, π sayısına ise çok yakın bir oran bulmuşlardı. Çinli bir matematikçi olan Liu Hui, çemberin içine ve dışına kenar sayıları giderek artan çokgenler çizerek çemberin çevresinin çapına oranını 3,1416 bulmuştu.
Liu Hui’den sonra döneminin dahilerinden olduğu düşünülen Zu Chongzui, 12.228 kenarlı bir çokgenden faydalanarak “227” oranını buldu. Bu oran sana tanıdık gelmiş olmalı. Daha sonra bu çalışmalarını daha da geliştirerek “355113” oranına ulaştı ve bu oran “Zu Oranı” olarak anılmaya başlandı.
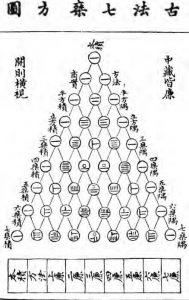
Savaş sanatları üzerine kitaplar yazan ve hem komutan hem de matematikçi olan Sun Tzu, rivayete göre ordularındaki asker sayılarını kısa bir zamanda saymak için çözüm yolları aramış ve bu arayışın sonunda “Çinli Kalan Teoremi”ni bulmuştur. Askerlerini 3, 5, 7 gibi asal sayılar kullanarak gruplamış ve kalan askerleri sayarak bütün askerlerin sayısına ulaşmıştır. Günümüzde de hala kullandığımız bu yöntem, modüler aritmetiğin temeli gibi görülebilir. Böylece anlıyoruz ki Çinliler geometri ve aritmetiğin yanında soyut cebir ile ilgili de çalışmalar yapmışlardır.
Çinli Kalan Teoremi
Yunanlılar gibi Çinliler de matematik içerisinde sırlar bulmaya çalışmış ve açıklayamadıkları matematiksel ifade ve şekilleri kutsal saymışlardır. Bunlardan biri de sihirli karelerdir. Sihirli kareler ile mutlaka karşılaşmışsındır. “Lo Shu Karesi” ya da “Dokuz Salon Diyagramı” olarak bilinen bu karenin özelliği satır, sütun ve köşegenlerindeki sayıların toplamının aynı olmasıdır. Müthiş değil mi? Kendi sihirli kareni yapmaya ne dersin? Mutlaka denemelisin!
Çinliler, aynı dönemde yaşadıkları uygarlıklara göre çok daha ileri bir matematik ile uğraşmaktaydı. Coğrafi konumlarından dolayı diğer uygarlıklar ile karşılaşamamış, bilgi aktarımı yapamamışlardır. Bu sebeple daha önce keşfetmiş olmalarına rağmen pek çok matematik teoremi başkalarının adıyla bilinmektedir. Çinlilerin matematik keşiflerini aktarma fırsatı olsaydı, çok önemli buluşlar yüzyıllar öncesinden yapılabilirdi.
Bir yolculuğumuzun daha sonuna geldik. Gelecek ay yeni yerlerde ve zamanlarda buluşmak üzere seni burada bekliyor olacağım! Sağlıkla Kal!
